Triple Decker
Purpose
Recently, in Angew. Chem. Int. Ed. 2002, 41, No. 9, Sheng Hua Liu et. al. reported the first successful synthesis and characterization of a triple-decker complex with a central metallabenzene (C37H54Ru3).
I thought it might be interesting to look at this novel structure from a Quantum Chemical perspective using visualization of orbitals and other properties. I also decided to visualize the difference between normal molecular orbitals and localized orbitals obtained via the Ruedenberg Method.
Calculation Details
pcGAMESS was used to calculate the energies, orbitals (delocailzed and localized), and density cubes for the triple-decker complex. Gaussian 98W was used to calculate the orbital and electrostatic cubes. gOpenMol and ArgusLab were used for initial visualization of orbitals, density, electrostatic potential, and electrostatic potential mapped onto the density. Final visualization for web presentation was done using POVRay for ray-traced and rendered images while a VRML client was used for VRML visualizations.
RHF closed shell molecular orbital calculations were performed on the +2 ion of the triple-decker complex at the experimentally determined geometry. We used the Hays, Wadt effective core potential and its associated minimal basis set of gaussian functions for the Ru atoms as well as its associated minimal basis set of gaussian functions for C and H. The experimental geometry looks like this:
A Ball and Stick Representation Of The Triple Decker Geometry
(Click on the image to download a 3D PDF representation. To view, open in Adobe Reader or equivalent.)
Orbital Localization
Application of the variation method to solve Schrödinger's equation yields a set of optimized cannonical molecular orbitals in which the electron density is delocalized (DMO) over the molecule as a whole. While these DMOs have the most direct experimental support through photo-electron spectroscopy (and are, therefore, also called spectroscopic orbitals), they frequently are not the most useful to the chemist who has found localized electron pairs extremely helpful in understanding chemistry. The superposition principle comes to the rescue of the chemist. Any linear combination of the cannonical orbitals is also a valid solution to Schrödinger's equation. This is the theoretical justification for hybridizing atomic orbitals and forming localized molecular orbitals (LMOs) from DMOs. 1
The most important reason for localizing orbitals is to analyze the wavefunction by visualizing orbitals and examining their Mulliken populations.
The method due to Edmiston and Ruedenberg works by maximizing the sum of the orbitals' two electron self repulsion integrals. Most people who think about the different localization criteria end up concluding that this one seems superior. 2,3 This is the localization approached used in this study.
Results
The following is a sample of the 149 Cannonical molecular orbitals that characterize the triple-decker complex
Top 11 Occupied Cannonical Orbitals Plus LUMO
Next, we find a sample of the Localized Molecular Orbitals:
Top 11 Localized Orbitals Plus LUMO
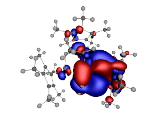
Also of interest is the charge distribution of the triple-decker complex. Here is a visualization of the electrostatic potential:
The 0.02 au Electrostatic Potential isosurfaces for the Triple-Decker complex.
Blue is the negative surface while red is the positive. We observe that negative electrostatic potential is interstitial to the ring systems while the positive electrostatic potential encompasses the rings and the central Ir atom.
Acknowledgements
Thanks to Guochen Jia for sending me a copy of the original paper and the associated CIF file containing the coordinates for the triple-decker complex.
References
- "Getting Accustomed to the Superposition Principle", Frank Rioux, Department of Chemistry,St. John's University, College of St. Benedict,St. Joseph, MN 56374
- "Localization tips", GAMESS User Manual
- C.Edmiston, K.Ruedenberg Rev.Mod.Phys. 35, 457-465(1963).