Water Dimer

PURPOSE:

Examine the water dimer system to determine what level of theory is necessary to determine the PES with chemically useful accuracy.

RESULTS:

Tools

All Hartree-Fock and Moller-Plesset (MP) results were calculated using the PC GAMESS version [1] of the GAMESS (US) QC package [2] . Density Functional results were calculated using Gaussian 98W [3].

Methods

Results were calculated using standard methods (i.e. Hartree-Fock (HF) and HF with correlation corrections from Moller-Plesset perturbation theory (MP2, MP3, MP4 SDQ, and MP4 SDTQ)). For all the MP calculations we used the entire space of occupied and virtual orbitals for the calculation. No orbitals were omitted. We also used two Density Functional methods (B3LYP and MPW1PW91) which explicitly include correlation effects at the SCF level of calculation.

1) Basis Sets

All basis sets used in this study were obtained from the Extensible Computational Chemistry Environment Basis Set Database [4]. Gaussian 98 basis sets were specified using the 6D 10F option to ensure basis set equivalence between the PC GAMESS and Gaussian calculations. Using the knowledge from our Neon analysis, all basis sets contain augmenting diffuse functions. The specific basis sets used (listed in terms of increasing completeness) were:

Basis Set Information

Click on the Designation for complete basis set information.

2) Linear Independence

Linear dependence problems can occur when using very large Cartesian gaussian basis sets augmented with many diffuse functions. The problem arises from the presence of linear combinations of Cartesian gaussian functions that are equivalent to other functions in the basis set (e.g. X2+Y2+Z2 is equivalent to an S type function). This equivalence violates the basic assumption that the basis set consists of a sum of functions that are independent of each other.

In this case, the problem was initially observed at the AUG-cc-pVQZ basis and required the removal of one s-type function (exponent value of 0.2067) from each Oxygen atom. Calculations were attempted using Dunning's AUG-cc-pV5Z basis but extensive linear dependence problems were observed. All attempts at their resolution resulted in basis sets that differed only marginally from the AUG-cc-pVQZ basis so these calculations were not performed.

3) Binding Energy Definition

The PESs are calculated from the Binding Energy at various geometrical configurations of the two water molecules. Binding Energy (BE) is defined as:

BE(counterpoise)=        Energy(dimer) 

- Energy(water1 + basis set of water2 (located at water2's position))

- Energy(water2 + basis set of water1 (located at water1's position))

Our definition of Binding Energy takes into account basis set superposition errors (BSSE). These errors arise from the fact that there are more basis functions used to represent the combined system than there are to represent the individual components. See our Neon results for more details. Note: throughout the rest of this document we will refer to this method of binding energy calculation as double counterpoise or DCP.

ANALYSIS:

1) Water Dimer Geometries

Eight water dimer geometries were established by fixing the Oxygen atom separation and then performing a complete optimization of all other geometrical parameters. These optimization calculations were carried out at the Hartree-Fock level of theory using the 6-31++G** basis set. These optimized geometries were used in all subsequent calculations.

Note: The purpose behind this method for selection of these geometries was to find a consistently chosen set of geometries to be used for the rest of our analysis. They do not (and are not intended to) represent the absolute best estimate of the geometry of the water dimer.

2) Basis Set Selection

We need to establish what basis set we must use to get meaningful results. Here are the dimer binding energy results at the HF level of theory:

It appears that the 6-31++G** is not the best choice for binding energy calculation for this system. 

Here are the results at the MP4 SDTQ level of theory:

It is clear that the 6-31++G** basis yields results that are incorrect relative to the other, more complete, basis sets. This is more easily seen in the following chart where we look at the variance of binding energies in the 6-31++G**, 6-311++G(3df,3pd), and AUG-cc-pVTZ results from those of the AUG-cc-pVQZ calculations.

From these results we find the 6-311. VTZ, and VQZ HF results differ little, one from the other, indicating these basis sets yield binding energy results increasingly closer to the limit of the Hartree-Fock method. The 6-31++G** is clearly not appropriate for use in this analysis. The VTZ and VQZ basis sets are the best, nearly equivalent, choices for this analysis.

Similarly, for the MP4-SDTQ results we find the binding energy variance to be:

Again, we see the inadequacy of the 6-31++G** basis. We also see the converging behavior of the Binding Energy as a function of increasing basis set completeness. The best results are obtained with the VTZ and VQZ basis sets.

Give the relatively small differences between the AUG-cc-pVTZ and AUG-cc-pVQZ results, we will use the AUG-cc-pVTZ basis for further analyses.

3) Method Selection

We also need to select the method to be used in future water dimer PES development. Here is a comparison of the various possibilities:

Obviously, the HF results are not acceptable. Let's look at the MP results by themselves:

These results are a bit odd. According to the theory, the results should increase in correctness from MP2 to MP3 to MP4 SDQ to MP4 SDTQ. Thus, we would expect the variances from the SDTQ result to be greatest for the MP2 method and the least for the MP4 SDQ method. As we see from the previous chart, the variances in the MP2 and MP3 are essentially equal with the MP4 SDQ variance being the largest. One might say this is a good thing because one could choose to use the MP2 method for the full PES with a significant reduction in computing requirements.

However, I am concerned that the small MP2 and MP3 variance might be just a fortuitous accident. Therefore, just to be safe, we will choose to use the MP4 SDTQ method for future PES calculations. We will continue to monitor the MP2 results just to see if additional data provides a clue to the reason for this low variance behavior.

4) Density Functional Methods

It is well documented that Density Functional Methods can provide quite good representations of some properties for chemical systems (including correlation effects) at a lower cost than the HF plus MP methods. We wanted to see if that was the case for the water dimer

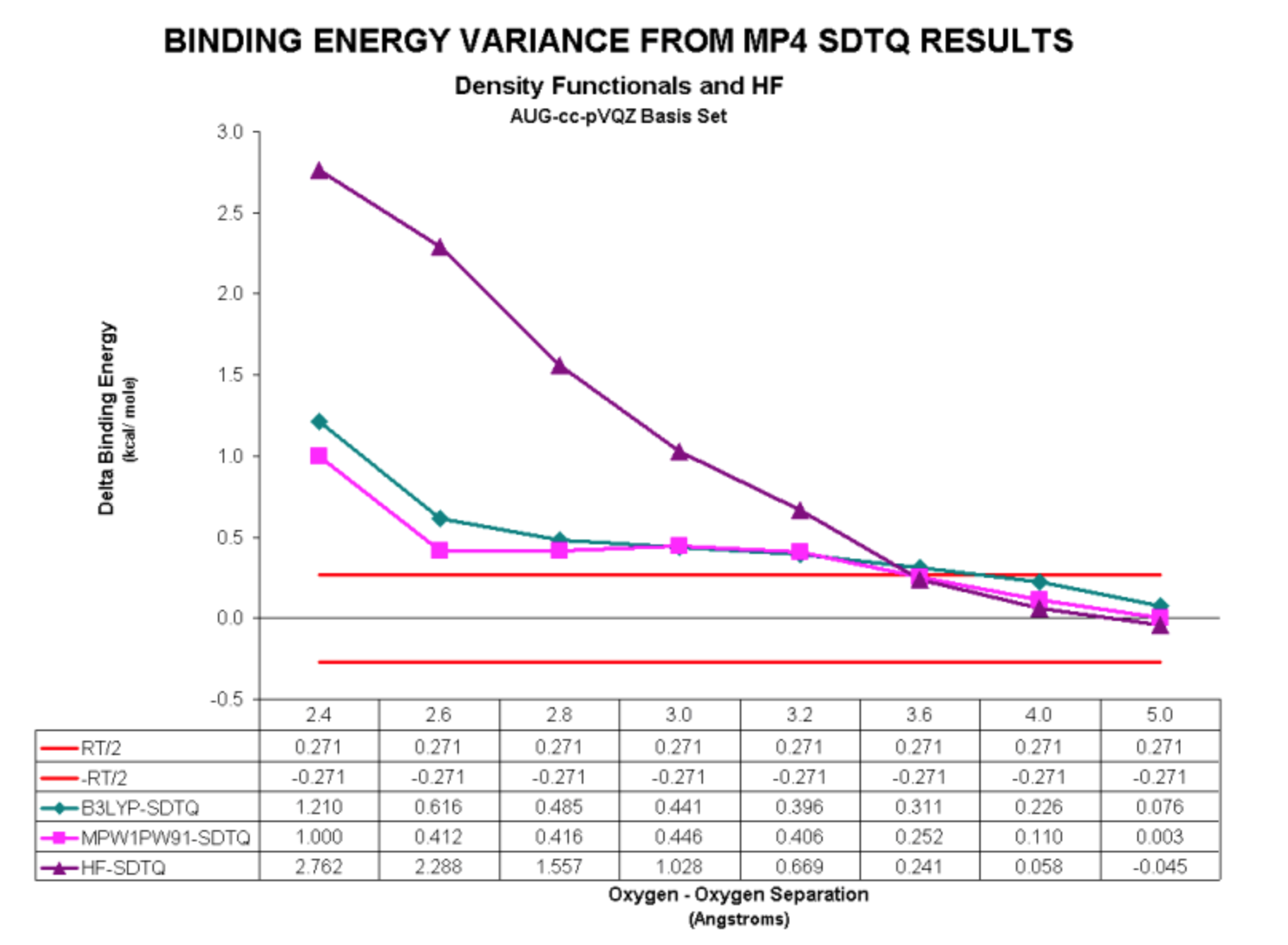
We performed a series of calculations using two Density Functional methods. The first, MPW1PW91, was shown to be the only DF method to provide physically reasonable results in our prior study on the Neon dimer. The other, B3LYP, was selected due to its popularity in the Quantum Chemistry field. Our results for these calculations are displayed below:

Here are the variances from the SDTQ results:

For the water dimer, the DFT methods yield a physically meaningful result.

5) Comparison with Molecular Mechanics Potential Energy Functions

In order to assess the utility of the results generated here, it would be reasonable to compare them with some of the principle Molecular Mechanics potentials currently used for large scale simulations of water and aqueous systems. One such water potential is the Tinker water potential, a polarizable multipole electrostatics model [5]. This model is equal or better to the best available water models for many bulk and cluster properties so it is the one we use for comparative purposes.

In the following chart, we present a comparison between the Tinker potential and those we have calculated (MP4 SDTQ and DFT):

The congruence of the MP4 SDTQ and Tinker potentials is remarkable, for Oxygen-Oxygen separations greater than 3.0 Angstroms. For separations less than 3.0 Angstroms, the agreement is less good with the Tinker potential being slightly more repulsive than the MP4 SDTQ results.

CONCLUSIONS:

From these results we conclude:

1. Use the MP4 SDTQ method. All of S,D,T and Q are required to get accurate results.
2. Use a substantial basis set with extensive polarization and diffuse functions, i.e. at least AUG-cc-pVTZ or better.
3. Counterpoise corrections are essential.
4. Our results compare well with those of more empirical potentials derived from experimental data.

NEXT STEPS:

Our plans for the future include the following:

1. Calculate a complete array of BE points for the water dimer using the AUG-cc-pVTZ basis set and the MP4 SDTQ method. At each point also calculate the charges at each atom (at the MP2 level).
2. Take a look at multibody effects on the BE and charge data at each point.
3. Fit that BE and charge data to a PES analytic function (probably of a type similar to the Tinker potential) with additional contributions for geometric variation/ deformation, charges as functions of geometry, and multibody effects.
4. Perform a series of Molecular Dynamics runs that examine the sensitivity of various bulk water properties to variabilities in the key attributes of the PES.

ACKNOWLEDGEMENTS:

My sincere thanks to Dr. Alex Granovsky for making the PC GAMESS source code available to me, for our many discussions regarding the use of PC GAMESS, MP4 SDTQ methods and the criticality of taking into account basis set linear dependence. Thanks also to Dr. Jay Ponder for his assistance with the use of the Tinker Molecular Mechanics software.

REFERENCES:

[1] Alex A. Granovsky, www http://classic.chem.msu.su/gran/gamess/index.html

[2] M.W.Schmidt, K.K.Baldridge, J.A.Boatz, S.T.Elbert, M.S.Gordon, J.J.Jensen, S.Koseki, N.Matsunaga, K.A.Nguyen, S.Su, T.L.Windus, M.Dupuis, J.A.Montgomery, J.Comput.Chem. 14, 1347-1363 (1993)

[3] Gaussian 98, Revision A.7,
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,
M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr.,
R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam,
A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi,
V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo,
S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui,
K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari,
J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu,
A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin,
D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara,
C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen,
M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon,
E. S. Replogle, and J. A. Pople,

[4] Basis sets were obtained from the Extensible Computational Chemistry Environment Basis Set Database, as developed and distributed by the Molecular Science Computing Facility, Environmental and Molecular Sciences Laboratory which is part of the Pacific Northwest Laboratory, P.O. Box 999, Richland, Washington 99352, USA, and funded by the U.S. Department of Energy. The Pacific Northwest Laboratory is a multi-program laboratory operated by Battelle Memorial Institute for the U.S. Department of Energy under contract DE-AC06-76RLO 1830. Contact David Feller or Karen Schuchardt for further information

[5] Tinker Molecular Mechanics v3.7, Jay William Ponder, Dept. of Biochemistry & Molecular Biophysics, Washington University School of Medicine, St. Louis, Missouri 63110 http://dasher.wustl.edu/tinker/ .